Module 3: Integers

• First read this page then start coding the module.
• Post your Python files to Blackboard under the Module 3 assignment.

Note: Create a text file called module3.txt where you will store you answers to exercise questions. The questions that are not related to changing code. You will submit this file on Blackboard along with your code.

Objectives

By the end of this module you will be able to:

• Create variable declarations.
• Assign values to variables by simple assignment, and print them out.
• Distinguish between integers in strings versus actual integers.
• Demonstrate ability to perform operations on integers for a desired output.
• Simplify expressions with constants to single value.
• Evaluate expressions with variables in them.
• Convert English descriptions of operations into expressions.
• Mentally trace execution with expressions and calculations.

First, an analogy

Suppose we have boxes. Consider the following rules about “boxes”:

• Each box can store only one item.

• The possible things that can be stored inside are called values.
• Thus, at any given moment, a box’s value is whatever’s inside it.
• Each box has a unique name:

There is a cloning process that works like this:

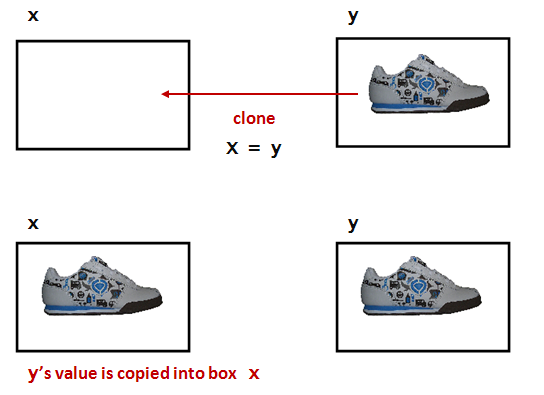
• The value inside one box is cloned.

• The cloned value is placed inside another.

• There is a strange shortcut notation to specify cloning:

x = y

• Here, the = (equals sign) does NOT mean “equals.”

• It has been repurposed to mean “clone”, “copy,” or, in programming-language jargon, “assign”.

• How to say it: “x is assigned the value in y”.

• Important: Remember, a box can hold only one value at a time.
• The technical term for our informal “box” is variable.

Integer Variables

We’ll now start working with “boxes” (variables) that hold integers (whole numbers like 3, 17, 2097, but not numbers like 3.141).

Consider this program:

i = 5
print(i)

Exercise 1: Type up the program in my_variable_example.py. Also save the file so that it can be submitted on Blackboard. What does it print? Report what you see in module3.txt.

Now let’s examine key parts of this program:

• First, i is the name of a “box” (of sorts).
• The term used for “box” is variable.
  • i is a variable.
• To put something in a variable, we use assignment
  • with the repurposed = (equals) sign.

    # i is the name of the variable 
    # that we've created
  
    i = 5  # 5 is the value that we're 
           # placing inside the variable i
  
    print(i)
  

• When we print a variable, what gets printed is its value.
  • Thus, the number 5 gets printed

    i = 5
    print(i)  # The value inside i 
              # (in this case, 5) gets printed
  

• Important: What you see on printed out is the number 5 and NOT the letter i
• Thus when you see print(i) you should think:
  • “Hmmm, the print function is going to print the contents of variable i”.
  • “I wonder what’s inside i?”
  • “Let me look in the program to see what was the most recent value that got written into i”.

• For example:

    i = 5
    i = 3
    print(i) 
  

Exercise 2: Type up the above in my_variable_example2.py and confirm that 3 is what gets printed.

By way of explanation:

i = 5
i = 3
print(i) # The most recent value of i (in this case, 3) gets printed

Exercise 3: Is it possible to not have a value in a variable? Consider this program:

i
print(i)

Type up the program in my_variable_example3.py What is the error? Answer in module3.txt. (Remember, non-coding questions are to be answered in your module text file, in this case: module3.txt.)

Thus: when you make a variable, you need to put something in it.

Next, let’s look at assignment between variables:

• This is the analogue of cloning between “boxes”.

• Consider this program:

    i = 5
    j = i     # The value in i gets copied into j
    print(j)  # Prints 5
  

We say, in short, “i is assigned to j”.

• Notice: we’ve used comments above to annotate and explain.
  • We’ll do this often, knowing that comments are not executed.

Exercise 4: Consider this program:

i = 5
j = i
print(j)
print(i)   # Did i lose its value?

Type up the program in my_variable_example4.py and report what gets printed in module3.txt.

The above example illustrates that the value in i gets copied into the variable j, which means that the value 5 is still in the variable i.

Exercise 5: Consider this program:

i = 5
j = i
k = j
print(k)

Try to identify the output of this program just by mental execution. Next, type up the program in my_variable_example5.py and confirm.

Exercise 6: Consider this program:

i = 5
j = i
i = 0
k = j
j = 0
print(k)

Try to identify the output of this program just by mental execution. Then type up the program in my_variable_example6.py and confirm.

Note that a copied value does not change if the original is changed:

• For example, consider:

    i = 5
    j = i      # j now has 5
    i = 0      # We changed i here
    print(j)   # j still has 5
  

• Here’s the line-by-line execution:
  • The first line puts the value 5 in variable i.
  • The second line copies the value in i (which is 5) into j. So j will have the value 5 as well.
  • The third line replaces the value 5 with value 0.
  • j still has 5, so the fourth line will print 5.
• Note: 0 is an actual value, and is not “no value” or “nothing”.

Exercise 7: Type up the following lines of code in my_variable_example7.py:

i = 5
j = 6      

# Add code between here

# and here.

print(i)   # should print 6
print(j)   # should print 5

Add some lines of code with the objective of swapping the values in variables i and j. You will need a third variable to be used as a holding place. Thus, without directly assigning the number 5 to j or the number 6 to i, write code using a third variable to achieve the desired swapping of values.

Integer Operators

Let’s examine the familiar arithmetic operators +, -, *, /

• Addition: +
• Subtraction: -
• Multiplication: *

• Division: /

• Consider this example with addition:

    i = 5
    j = 6
    k = i + j
    print(k)
  

• What happens during execution:
  • The values in i and j are added.
  • The resulting value goes into variable k.
• A long-ish way of saying this aloud:
  • “k is assigned the sum of the values of i and j”
    A shorter way:
  • “k is assigned i plus j”
• Here’s an example with multiplication and division:

    i = 5
    j = 6
    k = i * j
    print(k)      # prints 30
    m = i / j
    print(m)      # what does this print?
    n = i // j
    print(n)      # what does this print?
  

  ---

  Exercise 8: Type up the above in my_variable_example8.py. What is the value of n printed? Change i to 21. What is the value of n printed? Answer in module3.txt. Submit your code with i set to 5.

Integer division:

• In math, we learned that $1/4 = 0.25$ and $21/6 = 3.5$.
• This remains true in Python when we do something like

    i = 21
    j = 6
    m = i / j
  

• On the other hand, if we wish to perform integer division, we can use the integer division operator:

    i = 21
    j = 6
    m = i // j
  

• That is, the result is truncated down to the nearest integer.
  • Example: 3 // 2 becomes 1 because 1.5 gets truncated to 1.
  • Example: 15 // 4 becomes 3 because 3.75 gets truncated to 3.
• Integer division is useful when we want to do integer arithmetic.

Expressions and operator-precedence

Consider the following program:

i = 5
j = 6
k = i * j - (i + 1) * (j - 1)
print(k)

Exercise 9: Type up the above program in my_expression_example.py What does it print? Answer in module3.txt.

About expressions:

• An expression combines constants (like 1, above), and variables using operators.
• Example:

    i * j - (i + 1) * (j - 1)
  

• The above expression is really equivalent to:

    (i * j) - ((i + 1) * (j - 1))
  

  • Here, we added some clarifying parentheses.
• Operator precedence allows us to reduce the number of clarifying parentheses.
• Python precedence follows standard precedence in math: /, *, +, -.
• You might remember the precedence via the acronyms BODMAS or PEMDAS. (Look it up.)
• The above expression is NOT the same as:

    i * j - i + 1 * j - 1
  

Let’s dive a bit deeper into precedence and do some examples:

• We’ll use the four operators: add or +, subtraction or -, multiplication or *, and division or /.
• We’ll use plain ol’ numbers to illustrate.

• Note: The key to working them out is to use extra parentheses in the right way.

• The PEMDAS rule:
  • First apply Parentheses, then Exponents, then Multiplication and Division, and then Addition and Subtraction.
  • Example: 3 + 2*4
  • Here, we apply 2*4 to give 8
  • Then do 3 + 8 to give 11.
  • Applying extra parenthesis to 3 + (2 * 4) makes it clear.
• Example: 3*(24/3-2*3)
  • First, work out what’s inside the parens (the P of PEMDAS):
  • Do div to 24/3 and multiply to 2*3 to get (8 - 6)
  • This gives (2)
  • Now go out and see that we need to do 3*(2)
  • Which gives 6.
  • Using extra parens and spacing makes it clear: 3 * ( (24 / 3) - (2 * 3) )
• Example: 1 + ( (4 - 1) * 8) / 6
  • Do the innermost parens first: (4 - 1) = 3
  • Which results in 1 + (3 * 8) / 6
  • Then the next parens to give: 1 + 24/6
  • Then the D in PEMDAS: 1 + 4
  • Result: 5

Exercise 10: What does the expression i*j - i+1*j-1 evaluate to when i = 7 and j = 3? Answer in module3.txt.

More expressions

The remainder operator %:

• The expression 10 % 3 is “the remainder when 10 is divided by 3”.
• Thus 10 % 3 is 1.
• Similarly 11 % 4 is 3.
• The remainder operator is sometimes called modulo, as in “ten modulo 3 is 1”

Consider this example:

i = 14
j = -6
k = i % (-j)
print(k)

Exercise 11: Can you mentally execute and identify what’s printed? Type up the above in my_expression_example2.py to confirm. Report the value in module3.txt.